Ecuación de Van’t Hoff
En la mayoría de los casos la velocidad observada de una reacción química aumenta con el aumento de temperatura, más allá que la extensión de este aumento varíe mucho de reacción a reacción.
Conforme una antigua regla, la velocidad de una reacción aproximadamente dobla a cada aumento de 10ºC de temperatura (infelizmente la regla es tan aproximada que solo puede ser utilizada en un número limitado de casos). En términos de ecuación de velocidad, la causa de la variación de la velocidad de reacción con la temperatura reside en el hecho de que la constante de velocidad k varíe con la temperatura.
La relación entre ambas fue descubierta en 1887 por el científico Van’t Hoff e independientemente en 1889 por Arrhenius. Este último realizó un estudio extensivo de su aplicación en muchas reacciones.
Una descripción cuantitativa de la variación de una constante de equilibrio en la temperatura es descrita por la ecuación de Van’t Hoff.
La ecuación es:

Donde (Kp)1 es el valor de la constante de equilibrio para presiones a temperatura T1 y (Kp)2 es el valor de la misma constante pero a temperatura T2. R es la constante de los gases ideales y ΔHº es el calor de reacción o entalpía de reacción cuando reactivos y productos están en su estado estándar (para gases, 1 atm de presión y para soluciones 1 mol L-1, e ambos casos se asume un comportamiento ideal).
La ecuación de Van’t Hoff es comúnmente utilizada para determinar los valores de constantes de equilibrio a una cierta temperatura a partir de los valores de otra temperatura. También ofrece medios de obtener calores de reacción cuando las constantes de equilibrio son conocidas en dos temperaturas.
Otra forma de la ecuación de Van’t Hoff describe el cambio de la constante de equilibrio hacia la concentración Kc con la temperatura:

Observemos que esta fórmula contiene ΔUº en vez de ΔHº
La ecuación de Van’t Hoff está pareciendo familiar? Pues debería, porque es la versión general más actualizada de la ecuación de Clapeyron que describe la variación de la temperatura en función de la presión de vapor. La presión de vapor de un líquido es la constante de equilibrio Kp para el proceso:
Líquido <===> Gaseoso
En este caso la expresión de la ley de acción de las masas no tiene denominador porque el reactivo I es un líquido puro
Otras conclusiones de los estudios de Van’t Hoff
Van’t Hoff verificó una relación de semejanza entre la presión de los gases y la presión osmótica de las soluciones diluídas. Basado en las experiencias de presión osmótica de los estudiosos Pfeffer se constató una semejanza con las leyes de los gases de Boyle y de Charles:
“La presión osmótica de una solución es igual a la presión que el soluto ejercía en el estado gaseoso, ocupando el mismo volumen de la solución en la misma temperatura”.
Por tanto podemos aplicar la ecuación de los gases perfectos:
p . V = nRT
p = presión osmótica
V = volumen de la solución
n = cantidad en moles de soluto
R = constante de los gases perfectos
t = temperatura absoluta
Ecuación de la Presión Osmótica
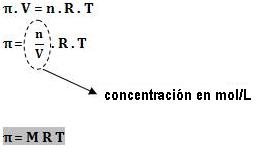
donde:
M = es la concentración en cantidad de materia (mol/L)
R = la constante de los gases perfectos
T = temperatura absoluta
Para presión en atmósfera, el valor de R será de 0,082 atm L . (mol . K)-1. Y para presión osmótica en milímetros de mercurio, el valor de R será de 62,3 mm Hg . L . (mol . K)-1.
Para soluciones iónicas, debemos utilizar el factor de corrección de Van’t Hoff:
i = α(q – 1) + 1
p = MRT . i
Como la presión osmótica depende de la concentración de partículas dispersas, es considerada una presión osmótica.
Llamamos como isotónicas a las soluciones con la misma presión osmótica. Cuando las soluciones osmóticas presentan diferencias son denominadas anisotónicas.
Las soluciones que presentan intensa presión osmótica son denominadas hipertónicas y las soluciones de presión osmótica débil son hipotónicas.
Factor de Corrección de Van’t Hoff
Observe que el número de partículas dispersas es equivalente al numero de moléculas disueltas multiplicado por el factor de corrección de Van’t Hoff representado por i.
Npd = Nd . i
Usando el ejemplo anterior tenemos:
190 = 100 . 1,9
Se demuestra entonces que:
I = 1 + α (q – 1)
Donde:
q = número de iones formado en la ionización de 1 molécula.
Aún sobre el mismo ejemplo:
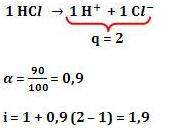
Observación:
Si α = 0, o sea, el soluto no sufre ionización, tendremos:
i = 1 + 0 (q – 1) = 1
Si α = 1, o sea, todas las moléculas ionizan, tenemos:
i = 1 + 1 (q – 1) = q
