Ecuación de Schrödinger

El físico austríaco, Erwin Schrödinger, desarrolló en 1925 la conocida ecuación que lleva su nombre. Esta ecuación es de gran importancia en la mecánica cuántica, donde juega un papel central, de la misma manera que la segunda ley de Newton en la mecánica.

Fue entre 1925 y 1930, cuando apareció la teoría de la mecánica cuántica, de la mano de un grupo de investigadores, donde destacaba Erwin Schrödinger. Esta teoría fue importante, no sólo por su relevancia e importante papel en la ciencia, sino también por la gran cantidad de conceptos científicos implicados en ella.

Son muchos los conceptos previos implicados en la ecuación de Schrödinger, empezando por los modelos atómicos. Dalton, Thomson, Rutherford, Bohr, todos ellos contribuyeron al modelo atómico actual, ideado por Erwin Schrödinger, modelo conocido como “Ecuación de onda”. Esta es una ecuación matemática que tiene en consideración varios aspectos:

• La existencia de un núcleo atómico, donde se concentra la gran cantidad del volumen del átomo.
• Los niveles energéticos donde se distribuyen los electrones según su energía.
• La dualidad onda-partícula
• La probabilidad de encontrar al electrón

A inicios del siglo XX se sabía que la luz podía comportarse como una partícula, o como una onda electromagnética, según las circunstancias, siendo el 1923, cuando De Broglie generalizó la dualidad a todas las partículas conocidas hasta el momento, proponiendo la hipótesis de que las partículas pueden ir asociadas a una onda, hecho que se comprobó experimentalmente cuatro años después, al observarse la difracción de electrones. En el caso de los fotones, De Broglie relacionó cada partícula libre con una energía E, con una cantidad de movimiento p, una frecuencia ν, y una longitud de onda λ, relacionandolas de la siguiente manera :

E = h ν

p = h / λ

Clinton Davisson y Lester Germer, realizaron la comprobación experimental, mostrando la longitud de onda relacionada a los electrones según la difracción siguiendo la fórmula de Bragg, que como había predicho De Broglie, se correspondía con la longitud de onda de su fórmula.

Schrödinger trató de escribir una ecuación siguiendo la anterior predicción de De Broglie pero reduciendo las escalas macroscópicas e la ecuación de la mecánica clásica, expresandose la energñia mecánica total como:

E= p^2 / 2m + V ( r )

Max Born dio una correcta interpretación física para la función de la función de Schrödinger en 1926, sin embargo el carácter probabilístico introducido por Schrödinger provocó mucha desconfianza en los físicos, incluso aquellos con renombre, como por ejemplo, Albert Einstein.

La solución de esta ecuación, fue la función de onda, siendo ésta, una medida de probabilidad de encontrar al electrón en un espacio, conocido como orbital.

Las funciones de onda se transforman con el tiempo, siendo su evolución temporal estudiada en la famosa ecuación del físico austríaco.

Otros conceptos utilizados por Schrödinger se basan en la óptica y la mecánica, y el paralelismo de ambas.

A inicios de los años 30, Born le dio una interpretación probabilística distinta a la función de onda a la que De Broglie y Schrödinger habían dado, lo que le supuso el premio Nobel. En este trabajo, Born vio mediante formulas matriciales de mecánica cuántica, que los conjuntos cuánticos de estados, de manera natural construían espacios de Hilbert, para poder representar los estados físicos en cuántica.

Actualmente la ecuación se formula según la mecánica cuántica, donde el estado en un instante t, de un sistema definido por un elemento │Ψ ( t ) > en el espacio de Hilbert, y usando la notación de Dirac , se pueden representar todos los resultados posibles de todas las medidas de un sistema.

Con la ecuación de Schrödinger describe la evolución temporal de │Ψ ( t ) > :

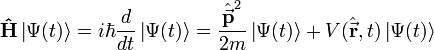
La ecuación también tiene limitaciones:

-No es una ecuación relativista, solamente puede describir partículas que tengan un momento lineal pequeño en comparación con la energía que tenga en reposo dividida por la velocidad de la luz.

-Esta ecuación no añade el espín en las partículas adecuadamente. Fue Dirac, más tarde, quien incorporó los espines a la ahora conocida como ecuación de Dirac, introduciendo además efectos relativistas.

Además de las limitaciones mencionadas, la ecuación de Schrödinger no puede describir sistemas con interacciones fuertes o débiles, como los que se encuentran en la física de partículas. Para estos casos, se utilizan teorías más avanzadas como la teoría cuántica de campos. Sin embargo, la ecuación de Schrödinger sigue siendo una herramienta fundamental en la física moderna, especialmente en la química cuántica y la física del estado sólido.

En la química cuántica, la ecuación de Schrödinger se utiliza para describir el comportamiento de los electrones en los átomos y moléculas. Esto permite a los científicos entender y predecir las propiedades químicas y físicas de las sustancias. Por ejemplo, la ecuación de Schrödinger se utiliza para calcular las energías de enlace, las estructuras moleculares y las propiedades espectroscópicas.

En la física del estado sólido, la ecuación de Schrödinger se aplica para estudiar las propiedades de los materiales. Esto incluye la conductividad eléctrica, el magnetismo y las propiedades ópticas. La ecuación de Schrödinger también es crucial en el diseño de dispositivos electrónicos, como los transistores y los semiconductores.

La ecuación de Schrödinger también ha encontrado aplicaciones en áreas fuera de la física y la química. Por ejemplo, en la biología molecular, se utiliza para estudiar la dinámica de las proteínas y el ADN. En la ciencia de materiales, se aplica para diseñar nuevos materiales con propiedades específicas.

A lo largo de los años, la ecuación de Schrödinger ha sido objeto de numerosas investigaciones y desarrollos. Se han propuesto muchas soluciones analíticas y numéricas para resolver la ecuación en diferentes contextos. Estas soluciones han llevado a avances significativos en nuestra comprensión de la naturaleza cuántica del universo.

En resumen, la ecuación de Schrödinger es una de las piedras angulares de la mecánica cuántica. A pesar de sus limitaciones, sigue siendo una herramienta invaluable para los científicos en una amplia variedad de campos. Su impacto en la ciencia y la tecnología continúa siendo profundo, y su legado perdurará en las futuras generaciones de investigadores.