El Potencial de Lennard-Jones
Una buena ilustración de la aplicabilidad del formalismo super simétrico aliado al método vibracional es obtenida del estudio del potencial de Lennard-Jones.
Este potencial está dado por:
![]()
Donde De es la energía de disociación y re es la distancia internuclear de equilibrio.
Con un poco de la manipulación algebraica es posible darse cuenta que la ecuación de Schrödinger radial para el potencial de la ecuación presentada, puede ser descrita de la siguiente forma:
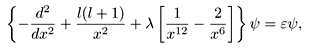
Donde 
corresponde al término de barrera de potencial
x =  ,
,
λ =  ,
,
y ε =  .
.
Por tanto, el Hamiltoniano para el potencial de Lennard-Jones está dado por:
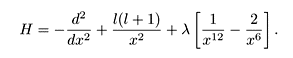
La solución exacta analítica para le ecuación de Schrödinger para este tipo de potencial no puede ser determinada. En tanto, puede buscarse un super potencial que provea un potencial efectivo similar al original y una auto-función apropiada para el método variacional. El superpotencial sugerido en este caso, tiene la forma:
![]()
Esta sugestión puede ser entendida mirando el potencial generado por el superpotencial anterior, con esta estructura se garantiza que los términos proporcionales a x-12, x-6 e x-2 aparezcan en el potencial efectivo. Con efecto, este superpotencial general el siguiente potencial efectivo a través de la expresión:
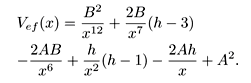
La auto-función es obtenida a través de otra ecuación y puede ser escrita como:
![]()
Donde h toma el papel de parámetro variacional
Comparando los términos proporcionales a 1/x12 y 1/x6 en las ecuaciones previas, con aquellos del potencial original, contenido en el hamiltoniano, es posible fijar los valores para las constantes A y B. En este caso, se tiene que A = B =  .
.
El autovalor de energía es obtenido a través de la minimización de una ecuación en relación al parámetro variacional h. Explícitamente, la ecuación a ser minimizada está dada por :
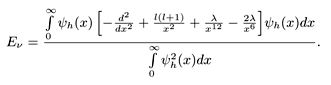
Los resultados de la minimización de la energía son mostrados en las Tablas 1 y 2.
En la Tabla 1 están presentados los resultados para l = 0 con diferentes valores de λ, en tanto en la Tabla 2 son mostrados los valores obtenidos para λ, fijo (10000), variando los valores de l. Los resultados son comparados con los valores encontrados en la literatura.
Tabla 1: Resultados numéricos para la energía del estado fundamental del potencial de Lennard-Jones para diferentes valores de λ para l fijo. Ev representa los valores obtenidos por el método variacional aliado a la super-simetría y EWKB son los valores encontrados a través del método WKB
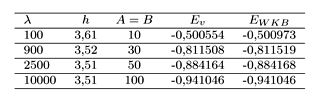
Tabla 2: Resultados numéricos para el potencial de Lennard-Jones para diferentes valores de l y para λ = 10000 (fijo). Ev representa valores obtenidos por el método variacional aliado a la super-simetría y EWKB son los valores encontrados a través del método WKB.

Los resultados presentados en las tablas muestran que los valores variacionales encontrados son equivalentes a los obtenidos por WKB. En la Tabla 1 se observa con exepción del primer resultado, los resultados coinciden hasta la 5ta casa decimal. Todos los valores de la Tabla 2 prácticamente coinciden.
La comparación gráfica entre los potenciales originales de Lennard Jones mas el termino de barrera de potencial efectivo, muestra la semejanza entre las dos curvas.
Un ejemplo de esta comparación es mostrado en la siguiente figura:
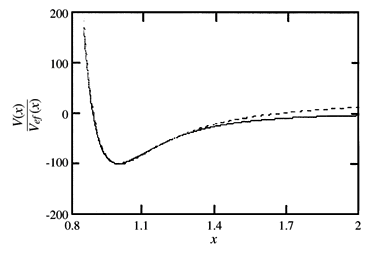
Figura: Comparación entre la curva del potencial original de Lennard-Jones, V(x) es el potencial efectivo sugerido Vef (x). Los parámetros usados son λ = 100, A = 10, B = 10 y h = 3,61.
