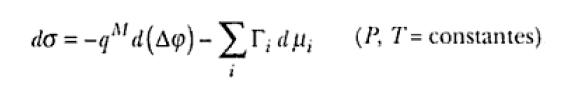La doble capa eléctrica
La región fronteriza entre dos fases con composiciones distintas está caracterizada por la presencia de fuerzas anisotrópicas. Un ejemplo común donde esto sucede es la interfase agua/aire, resultando en la aparición de fenómeno de tensión superficial del agua.
Una molécula del agua al interior de un bécquer conteniendo el líquido interactúa con las moléculas vecinas de forma homogénea, dentro de una misma región esférica centrada en esta molécula, siendo que las fuerzas de interacción no dependen de la dirección (fuerzas isotrópicas). En tanto, la situación de una molécula situada en la superficie del líquido y en contacto con el aire es diferente.
En la semiesfera situada debajo de la superficie, la molécula interactúa con otras moléculas de agua y en la otra el contacto se establece con las moléculas de las especies que forman el aire. Y es de esta anisotropía de fuerzas que surge el fenómeno de la tensión superficial y las demás propiedades características de la interfase.
Considerando ahora un soluto iónico disuelto en agua, se observa que el comportamiento de un ión presenten en el interior de la solución es gobernado por fuerzas isotrópicas, en tanto que el comportamiento del ión cerca de la superficie es gobernado por fuerzas anisotrópicas. Así, si la concentración de este ión fuese mapeada en función de su posición, se verifica que al interior de la solución ella es siempre constante.
Por otra parte, dependiendo del componente total de las fuerzas anisotrópicas superficiales en las regiones próximas a la interfase, habrá un aumento o una disminución de la concentración del ión.
En este caso, como especies cargadas eléctricamente están involucradas, el resultado será una distribución desigual de cargas eléctricas de la cual se sigue la aparición de una diferencia de potencial entre la superficie y el interior de la solución. En el caso de las moléculas de agua del ejemplo anterior y siendo ellas dipolos eléctricos, también se observará que la distribución de potenciales no será uniforme debido a fuerzas anisotrópicas, promoviendo una orientación preferencial de estos dipolos.
En una interfase electrodo/solución electrolítica, los fenómenos ocurren de forma semejante al que ya fue descrito, apenas en el hecho de que la caída de potencial entre el electrodo y la solución puede ser controlada a través de un circuito externo.
La región fronteriza en este caso es denominada como doble capa eléctrica. En la ausencia de factores externos, la anisotropía de fuerzas, incluyendo las fuerzas electroestáticas presentes en esta interfase, resulta una acumulación o carencia de determinadas especies sobre la superficie interfacial en relación al medio de la solución (adsorción). Adicionalmente, se debe tomar en consideración que en las interfases electrodo/solución es posible imponer una diferencia de potencial variable a través de una fuente externa.
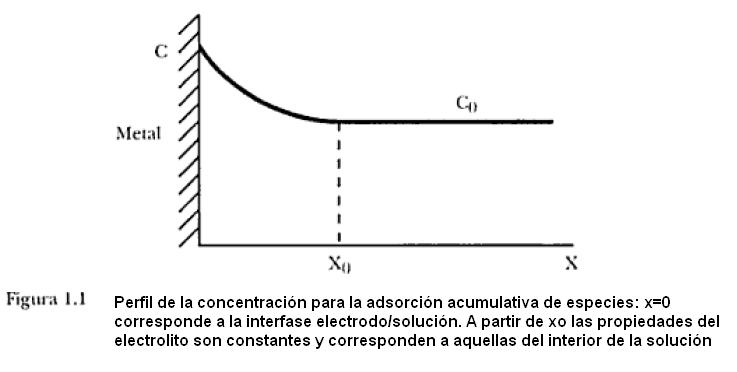
Esto permite controlar extremadamente la adsorción de cargas y dipolos. El perfil aproximado de la variación de la concentración de una especie para el caso de la adsorción acumulativa es presentado en la figura 1.1.
Para interfases no sometidas a perturbaciones externas, la descripción cuantitativa de la adsorción en la superficie de separación interfasial puede ser realizada termodinámicamente a través de la ecuación de Gibbs, o sea:
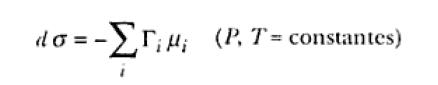
donde σ es la tensión superficial o sea, el trbajo superficial reversible necesario para aumentar la superficie de separación interfasial en una unidad de área; μi es el potencial químico del componente i y Гi es una magnitud interfasial denominada como exceso superficial, en este caso también del componente i. Esta magnitud nada más es que la cantidad de especies i que debe ser introducida en el sistema para que la composición de la fase volumétrica se mantenga constante al aumentarse en una unidad la superficie interfasial.
Es importante notar la diferencia que existe entre Гi y la concentración superficial Ci, o sea, la cantidad del componente i absorbido por unidad de área, o mismo entre Гi y la concentración volumétrica Ci que es la cantidad de componente i por unidad de volumen. Simplificándolo;
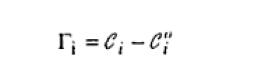
O en términos del gráfico de la Figura 1.1 (grafica)
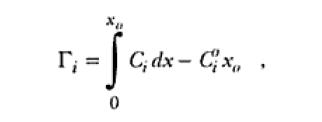
donde Ci0 es la concentración de la especie i al interior de la solución contenida en una franja de espesor igual a la doble capa (xo) y expresada en moles por unidad de área y Ci0 la concentración de la misma especie también al interior de la solución, sin embargo, expresada en moles por unidad de volumen. De esta forma el exceso superficial caracteriza la variación de la composición de la capa superficial en comparación con la de un sistema en el cual la concentración se mantiene uniforma hasta el plano que define la interfase (x=0 en la Figura 1.1). Para calcular la concentración superficial de una especie y a partir de esta el exceso superficial, es necesario adoptar modelos para la doble capa.
La adsorción de especies en la interfase electrodo/solución involucra tanto iones cuanto dipolos. En la Figura 1.2 se ilustra esta situación, para el caso de un electrodo conteniendo cargas superficiales (qM) positivas, observándose también que, debido a la presencia de cargas en el metal, la distribución no uniforme de iones y la orientación preferencial de dipolos, ocurre una diferencia de potencial eléctrico (Δφ) entre el metal y la solución electrolítica.
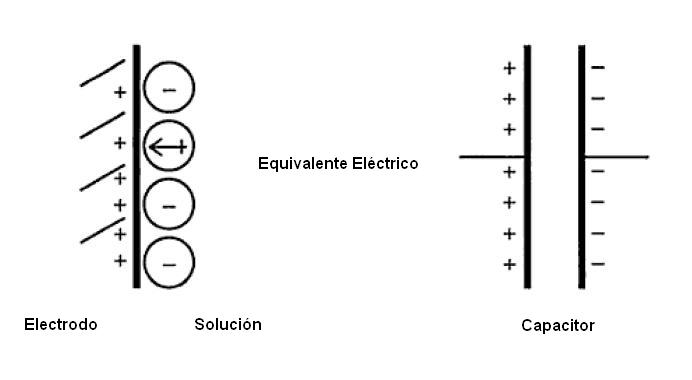

Debido a estos componentes eléctricos es visto que pueden ser controlados externamente, conforme será estudiado más adelante en la ecuación de Gibbs no puede ser directamente empleada en la formulación de los fenómenos de la doble capa, pues ella no incluye el trabajo eléctrico que contribuye a determinado valor de la tensión superficial.
Para considerar esa contribución es necesario observar que en la ausencia de transferencia de la carga a través de la interfase la condición termodinámica de equilibrio exige que la interfase sea eléctricamente neutra. Esto equivale a decir que a una dada carga en el electrodo corresponderá una carga igual y de signo opuesto en la solución. Así, en su forma más simplificada, la interfase puede ser considerada como un capacitor de placas paralelas (Figura 1.2). Utilizando este modelo simple de capacitor de la Figura 1.2 se observa que este trabajo puede ser expresado por el producto de la carga por el diferencial de la diferencia de potencial entre las placas, o sea – qMd (Δφ). Introduciéndose este término en la ecuación de Gibbs, se obtiene: