Invariancia de escala

En un recipiente con agua a punto de hervor, las burbujas de vapor, nucleadas en el fondo del recipiente, crecen, se liberan, y fluctúan hasta la superficie de donde se escapan para la atmósfera. A la temperatura de ebullición, el agua existe al mismo tiempo en dos fases distintas – líquido y gas – y a medida que las burbujas se forman las dos fases se separan en el espacio. Si cerramos el recipiente la temperatura de ebullición aumenta, como en una olla a presión. A medida que la presión aumenta, el sistema llega al punto crítico, donde las propiedades del líquido y del gas se vuelven idénticas. Por encima de esa temperatura, en el régimen supercrítico, dejan de existir dos fases distintas y existe apenas un fluido homogéneo.
Cerca del punto crítico, la materia fluctúa sin límites. Burbujas y gotas, unas tan pequeñas como unos cuantos átomos, otras tan grandes como el recipiente, aparecen y desaparecen, se unen y se separan. Exactamente en el punto crítico la escala de las mayores fluctuaciones divergen, pero el efecto de las fluctuaciones en escalas menores no es despreciable. La distribución de las fluctuaciones es invariable para transformaciones de escala.
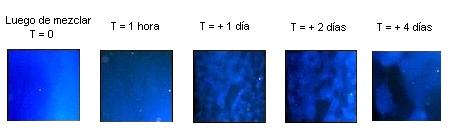
Fluctuaciones en una mezcla coloidal cerca del punto crítico
En el punto crítico, la tasa de variación de las funciones termodinámicas diverge. Estas divergencias adoptan la forma de leyes de potencia con exponentes (los exponentes críticos) que dependen sólo de algunas características del sistema. En el punto crítico el sistema es invariable para transformaciones de escala.
La invariancia de escala es un fenómeno que se observa no sólo en la física y la química, sino también en una variedad de campos, incluyendo la biología, la geología y la economía. Por ejemplo, en la biología, los patrones de ramificación de los árboles y las venas en las hojas a menudo muestran invariancia de escala. En la geología, las formas de las montañas y las costas pueden ser descritas por fractales, que son formas geométricas que son invariantes a la escala. En la economía, la distribución de los ingresos y la riqueza a menudo sigue una ley de potencia, que es una forma de invariancia de escala.
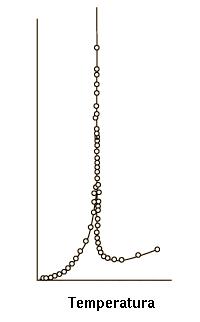
Calor específico del helio cerca del punto crítico
La hipótesis de invariancia de escala, que surgió en el contexto de los fenómenos críticos, dio origen a dos categorías de previsiones, ambas verificadas experimentalmente para una gran variedad de sistemas. La primera categoría es un conjunto de expresiones, llamadas relaciones de escala, que implican los exponentes críticos que caracterizan el comportamiento singular de los sistemas críticos. La segunda categoría implica un ‘colapso’ o reducción de los resultados experimentales. De hecho, se verifica que próximo al punto crítico, las funciones termodinámicas de n variables pueden ser representadas por funciones de n-1 variables debidamente escaladas. Estos principios de la invariancia de escala han sido útiles en la interpretación de muchos más fenómenos, desde la formación de galaxias hasta los mercados financieros y a la sociología.
A principios de los años 70, K. Wilson propuso una teoría para los fenómenos críticos basada en una alteración esencial de un método largamente utilizado en Física Teórica, llamado teoría del grupo de renormalización. La teoría que Le valió a Wilson el Premio Nobel de Física en 1982 permitió la descripción del comportamiento de los sistemas próximos al punto crítico, incluyendo el cálculo de las cantidades esenciales que caracterizan la transición (los exponentes críticos). Uno de los resultados más importantes de esta teoría es la precisión de la existencia de clases universales (tipos de criticalidad caracterizados por conjuntos de exponentes) que no dependen de los detalles de las interacciones microscópicas, pero sólo de su simetría.
La invariancia de escala también se ha observado en sistemas dinámicos, como los sistemas de partículas en interacción. En estos sistemas, la invariancia de escala puede manifestarse en la forma de leyes de potencia para la distribución de tamaños de los cúmulos de partículas. Este fenómeno ha sido observado en simulaciones de computadora de sistemas de partículas en interacción, así como en experimentos con coloides y suspensiones de partículas.
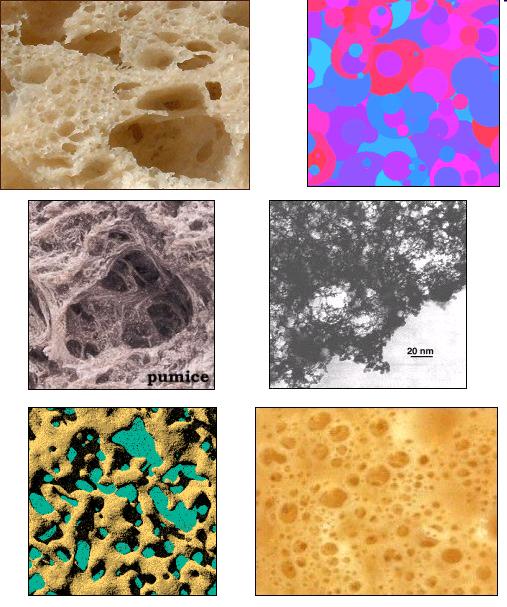
Algunas estructuras con una simetría parecida a la de un fluido en el punto crítico: feta de pan, representación de las fluctuaciones en el barrio del punto crítico, piedra pómez, aerogel, modelo de Ising tridimensional por debajo de la temperatura crítica y espuma de cerveza, respectivamente.
