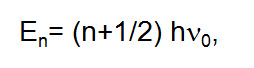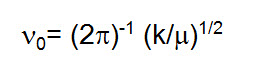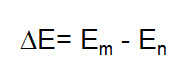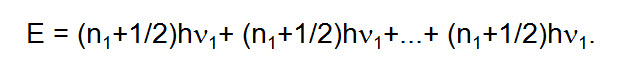Vibración molecular – Espectroscopia Vibratoria
Se denomina espectroscopia vibratoria a la técnica de análisis en la cual se utiliza radiación electromagnética para testear el comportamiento vibratorio de moléculas observándose la absorción o esparcimiento de esa radiación.
Desde que las energías vibratorias de las moléculas se encuentran en una franja de 0 a 60 kJ/mol, la absorción de la radiación se presenta en la franja infrarroja, entre 0 e 5000 cm-1, en una de las autofrecuencias de los grupos moleculares, si el modo vibratorio modifica el largo del dipolo eléctrico correspondiente. La observación directa de la absorción de radiación por vibraciones moleculares es por tanto un experimento de espectroscopia del infrarrojo.
Las vibraciones moleculares también pueden ser estudiadas por un experimento de esparcimiento de radiación, usualmente en la franja de la luz visible. En este tipo de experimentos la energía de la radiación incidente es levemente modificada por la interacción inelástica con los modos de vibración. La observación del esparcimiento de luz por vibraciones moleculares, se denomina Espectroscopia Raman.
La completa comprensión de la espectroscopia vibratoria solo es posible en el contexto de la mecánica cuántica. La solución cuántica del problema del oscilador armónico simple prevé valores discretos para la energía vibratoria, los cuales están dados por:
Donde n es un número natural llamado número cuántico vibratorio, h es la constante de Planck y
Es la frecuencia del oscilador armónico clásico, k es la constante elástica y μ la masa reducida.
La energía del oscilador armónico cuando n=0 (el estado vibratorio fundamental) es conocida como la energía del punto cero.
En un experimento de espectroscopia se estudian las transiciones entre los estados vibratorios cuantizados. A diferencia de la energía involucrada en la transición del estado vibratorio n par el estado m es:
Y la intensidad de la línea de absorción está relacionada a la probabilidad de una transición
n —> m
El conjunto de las probabilidades de transición entre los posibles estados n y m es conocido como el conjunto de las reglas de selección para las transiciones.
En el caso de una molécula di atómica solo ocurre absorción de energía (y por tanto transición entre dos estados vibratorios) si:
1- Hubiese cambio en el valor del dipolo eléctrico de esa molécula (p= Qr, donde Q es la diferencia de carga entre los centro atómicos y r es la distancia entre ellos).
2- El número cuántico vibratorio cambia por una unidad, i.e. Δn = ±1
Esas reglas de selección son válidas apenas como primera aproximación pues, como se sabe, el potencial interatómico no es perfectamente armónico. La solución cuántica del problema del oscilador anarmónico prevé niveles de energía separados por diferencias de energía decrecientes a medida que aumenta el número cuántico vibratorio.
Las vibraciones de moléculas poliatómicas acostumbran ser analizadas tratando cada modo normal de vibración como un oscilador independiente con sus propios niveles de energía. La energía vibratoria total de la molécula es entonces calculada como la suma de la energía de los osciladores individuales.
La introducción de anarmonicidad en el estudio del comportamiento vibratorio de moléculas poliatómicas hace con que las formas normales no puedan ser tratadas más como independientes.
Las reglas de selección obtenidas anteriormente para el caso de una molécula diatómica, pueden ser extendidas a moléculas poliatómicas. En general, para que una vibración sea activa para absorción de radiación infrarroja, el movimiento de vibración debe causar un cambio en el momento del dipolo inclusive cuando la molécula no tenga el momento del dipolo permanente (la molécula de CO2, por ejemplo es apolar y tiene dos vibraciones activas en el infrarrojo)
La complejidad del problema de estudiar el espectro vibratorio de moléculas poliatómicas puede ser bastante reducida cuando se exploran las propiedades de simetría de las moléculas, lo cual se realiza como un auxilio de la teoría matemática de los grupos de simetría.